Introduction

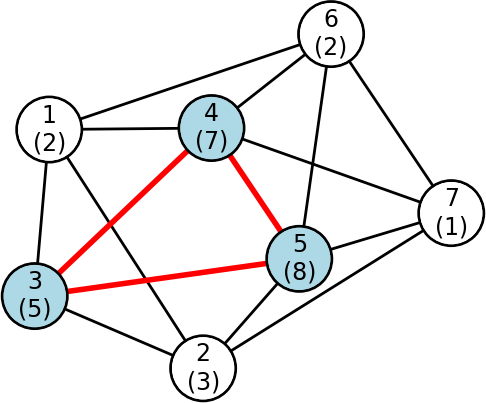
• MaxCliqueWeight (and its variant MaxCliqueDynWeight) is a new exact algorithm for identifying a maximum weight clique in a weighted undirected graph. The algorithm uses an efficient branch-and-bound approach with a new weighted graph coloring algorithm that efficiently determines upper weight bounds for a maximum weighted clique in a graph.
• A maximum weight clique is a fully connected subgraph of a graph with the highest sum of its vertex-weights.
• We evaluated the algorithm on random weighted graphs with node counts up to 10,000 and on standard DIMACS benchmark graphs used in a variety of research areas. We find a remarkable improvement in computational speed when compared to existing algorithms, particularly evident in the case of high-density random graphs and DIMACS graphs, where our newly developed algorithm outperforms existing alternatives by several orders of magnitude.

Download & Installation

• To install the latest version of the MaxClique(Dyn)Weight algorithm follow this link.
• Weighted graphs that were used in the paper for testing the algorithm are available on the links below. Graphs have integer vertex weights. In the first version of graphs (first and second in the list), each graph's vertices were shuffled 100x to test the algorithm's performance with different initial vertex orderings. In the second version of graphs (third and fourth in the list), for random graphs, for each particular size and density, 100 random graphs were generated; for DIMACS graphs, each was assigned random weights 100x.
  Graph files:
  • Random weighted graphs (vertices shuffled 100x)
  • DIMACS weighted graphs (vertices shuffled 100x)
  • Random weighted graphs (randomized edges&weights 100x)
  • DIMACS weighted graphs (randomized weights 100x)

Please Cite

• Kati Rozman, An Ghysels, Dušanka Janežič and Janez Konc. An exact algorithm to find a maximum weight clique in a weighted undirected graph. In preparation.